Array
Problems listed in the order of difficulty. * denotes in top interview questions.
Easy
- 001 Two sum * (note)
- 009 Palindrome Number (note)
- 035 Search Insert Position (note)
- 036 Validate sudoku * (note)
- 026 Remove duplicates from sorted array * (note)
- 027 Remove Element (note)
- 048 Rotate image * (note)
- 066 Plus one * (note)
- 119 Pascal’s Triangle II ((note)
- 122 Best Time to Buy and Sell Stock II *((note)
- 136 Single number * (note)
- 167 Two Sum II - Input array is sorted (note)
- 169 Major Elements (note)
- 189 Rotate array * (note)
- 217 Contains duplicates * (note)
- 283 Move zeros * (note)
- 350 Intersection of two arrays II * (note)
Hard
Solve array problem with Fenwick Tree
(Refer to Hackerearth Fenwick tree tutorial))
Given array \(a[ ]\),
- Problems:
- change the value at index \(i\)
- find sum of prefix of length \(k\)
- Goal: want tasks finished in \(O(logN)\) time
bit manipulation trick :isolating the last set bit (last set bit: 最末一个值为1的bit)
Answer: x & (-x) gives the last set bit in a number:
i.e. -x = 2’s complement of x = (a1b)’ + 1 = a’0b’ + 1 = a’0(0….0)’ + 1 = a’0(1…1) + 1 = a’1(0…0) = a’1b (-x 即是 x 的补码, 即 x 取反+1) e.g. x = 10 = b’1010’, x & (-x) = 1010 & 0110 = 0010 = 2
Binary Index (Fenwick) Tree (BIT):
- At any index, we store the sum of some numbers in the array
e.g. we have a = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16]
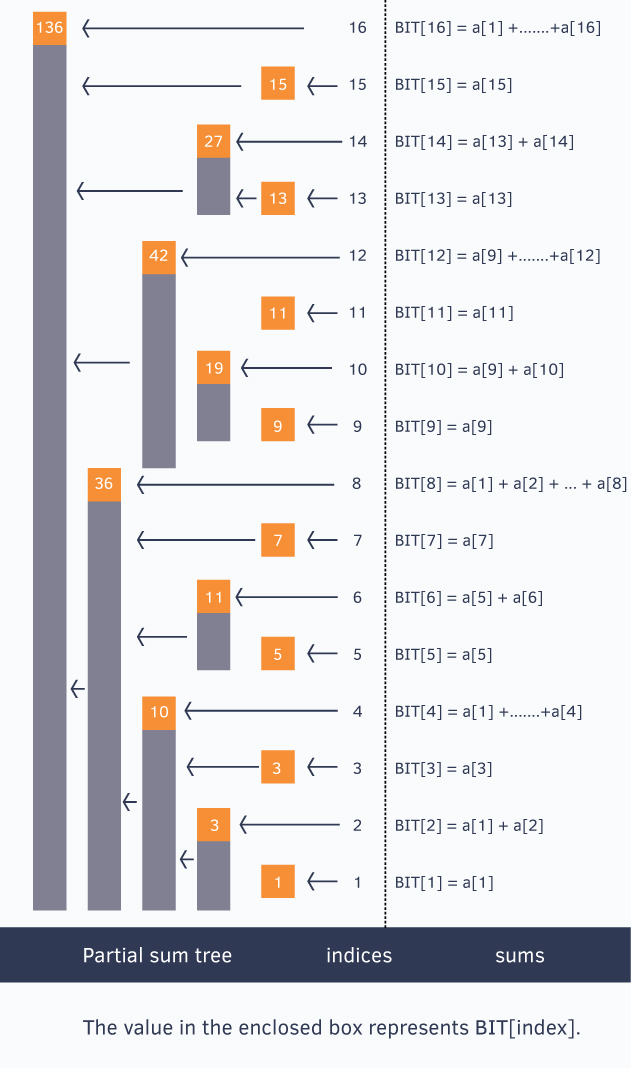
BIT[x]奇数位存当前值, 2的次放数位存截止到目前位数和
To generalize this every index \(i\) in the BIT[] array stores the cumulative sum from the index \(i\) to \(i-(1<<r)+1\) (both inclusive), where \(r\) represents the last set bit in the index .
e.g. sum of first 12 numbers in array:
\(a[] = BIT[ 12 ] + BIT[ 8 ] = (a[ 12 ] + … + a[ 9 ]) + (a[ 8 ] + … + a[ 1 ])\)
BIT[] is an array of size = 1 + sizeof(array a[]), and is initialized with all values equal to 0.
def update(x, val, BIT):
while x <= n:
BIT[x] += val
x += x&(-x) # by incrementing x this way, we update all the slots that contain values including x
If we look at the loop in update() operation, we can see that the loop runs at most the number of bits in index which is restricted to be less or equal to N (the size of the given array), so we can say that the update operation takes at most \(O(logN)\) time.
def sum(x):
sum = 0
while x > 0:
sum += BIT[x]
x -= x&(-x)
return sum
A complete FenwickTree class:
class FenwickTree(object):
def __init__(self, n):
self.n = n
self.tree = [0] * (n + 1)
def lowbit(self, x):
return x & -x
def update(self, x, val): # update value at each index
while x <= self.n:
self.tree[x] += val
x += self.lowbit(x)
def sum(self, x): # return sum of first x elements
res = 0
while x > 0:
res += self.tree[x]
x -= self.lowbit(x)
return res
Application: Leetcode Problem 683 K empty slots